Heute erläutern wir den Sieb des Eratosthenes anhand einer beispielhaften, vereinfachten, Implementierung in PowerShell. Beim Sieb des Eratosthenes handelt es sich um ein Verfahren zur Bestimmung aller Primzahlen bis zu einer vorgegebenen Zahl. Die Zahlen werden von Klein nach Groß durchgegangen und alle Vielfachen werden jeweils elimiert. Das führt dazu, dass ausschließlich Primzahlen übrig bleiben.
Beispiel
Wenn wir bspw. einen Zahlenstrahl von 2 bis 100 sieben wollen, so starten wir zunächst mit der 2. Diese wird als Primfaktor erkannt, woraufhin alle Vielfachen gestrichen werden, also 4,6,8,10,12 usw.
Sind alle Vielfachen der 2 eliminiert, fahren wir mit der 3 fort. Also werden 6,9,12,15,18,21 usw. gestrichen. Hierbei können die bereits als Vielfache von 2 identifizierten, also bereits gestrichenen, Zahlen natürlich übersprungen werden. Anschaulich visualisiert sieht das so aus:

Von https://en.wikipedia.org/wiki/de:User:SKopp“ als eigenes Werk im deutschen Wikipedia veröffentlich
Implementierung
Zahlenstrahl
Lasst uns das Ganze nun Step-by-Step als Programm umsetzen.
Hierfür definieren wir als erstes unsere Endzahl, also die Obergrenze des Zahlenstrahls den wir sieben möchten, sowie die Wurzel dieser Zahl. Denn wenn wir die Vielfachen aller Zähler, welche größer als die Wurzel der Zahl sind, eliminiert haben sind alle übrigen Elemente automatisch Primzahlen.

Wie anfänglich gesagt geht es um eine stark vereinfachte und keinesfalls optimierte Variante. Wir „streichen“ also als erstes die 1, damit diese abschließend nicht in der Ausgabe unserer Primfaktoren erscheint:
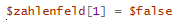
Durchlauf der potenziellen Primfaktoren
Nun benötigen wir zunächst eines äußere Schleife in der wir alle Potenziellen Primfaktoren, also die Zahlen von 2 bis zur Wurzel unserer Endzahl durchlaufen, gefolgt von einer Prüfung, ob die betreffende Zahl bereits „gestrichen“ wurde:

Streichen der Vielfachen
Ist die Zahl noch nicht als Vielfaches eines vorangegangenen Primfaktors erkannt und somit noch im Rennen, so streichen wir ihre Vielfachen:

Hierbei beginnen wir absichtlich mit dem zweifachen des Primfaktors, sodass dieser selbst in unserem Zahlenstrahl verbleibt.
Ausgabe des gesiebten Zahlenstrahl
Abschließend erfolgt eine Ausgabe aller verbliebenen Zahlen:
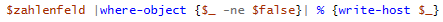
Inklusive der Ausgabe aller gefundenen Primzahlen, sowie der benötigten Laufzeit ergibt sich dann folgendes kleine Script:
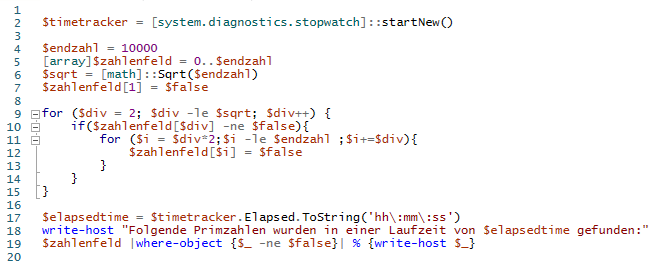
Optimierungen
Um die Laufzeit und die Speichernutzung zu optimieren gibt es hier nun unterschiedliche Optimierungsansätze. Der erste, einfachste und effektivste wäre es alle geraden Zahlen bereits beim Aufbau des Zahlenstrahls außenvor zu lassen. Bei einem so kleinen Zahlenstrahl wie in unserem Beispiel fällt der Unterschied nicht wirklich auf, wenn man jedoch eine deutlich größere Menge Zahlen sieben möchte, so ist der Unterschied immens. Denn hier gilt die ersten Durchläufe benötigen am längst, da hier, wie oben in der Grafik schön abgebildet ist, die meisten Zahlen gestrichen werden müssen. Mit zunehmendem Fortschritt wird das Streichen der Vielfachen immer schneller und schneller.
Hat Euch dieser Beitrag gefallen? Dann lasst uns doch einen Like auf Facebook oder Instagram da, oder kommentiert einfach direkt hier! Schickt uns gerne Eure Implementierungen oder Verbesserungsvorschläge des Sieb des Eratosthenes. Welche Siebe kennt Ihr noch ? Habt ihr Interesse an einer schematischen Implementierung des Atkins Sieve? Schreibt uns!


















